In this recitation, we covered problems from “Solids of Revolution” and the Ximera homework.

Solids of Revolution

Building off of the ideas from last time, we’re now going to consider what happens when we revolve a shape around an axis. There are two sort of “approaches” to doing this that we wish to consider. As a model, let’s think about the region bounded between \(y = \frac{1}{3} \ln(x)\), \(x=e^3\), and \(y= 0\).

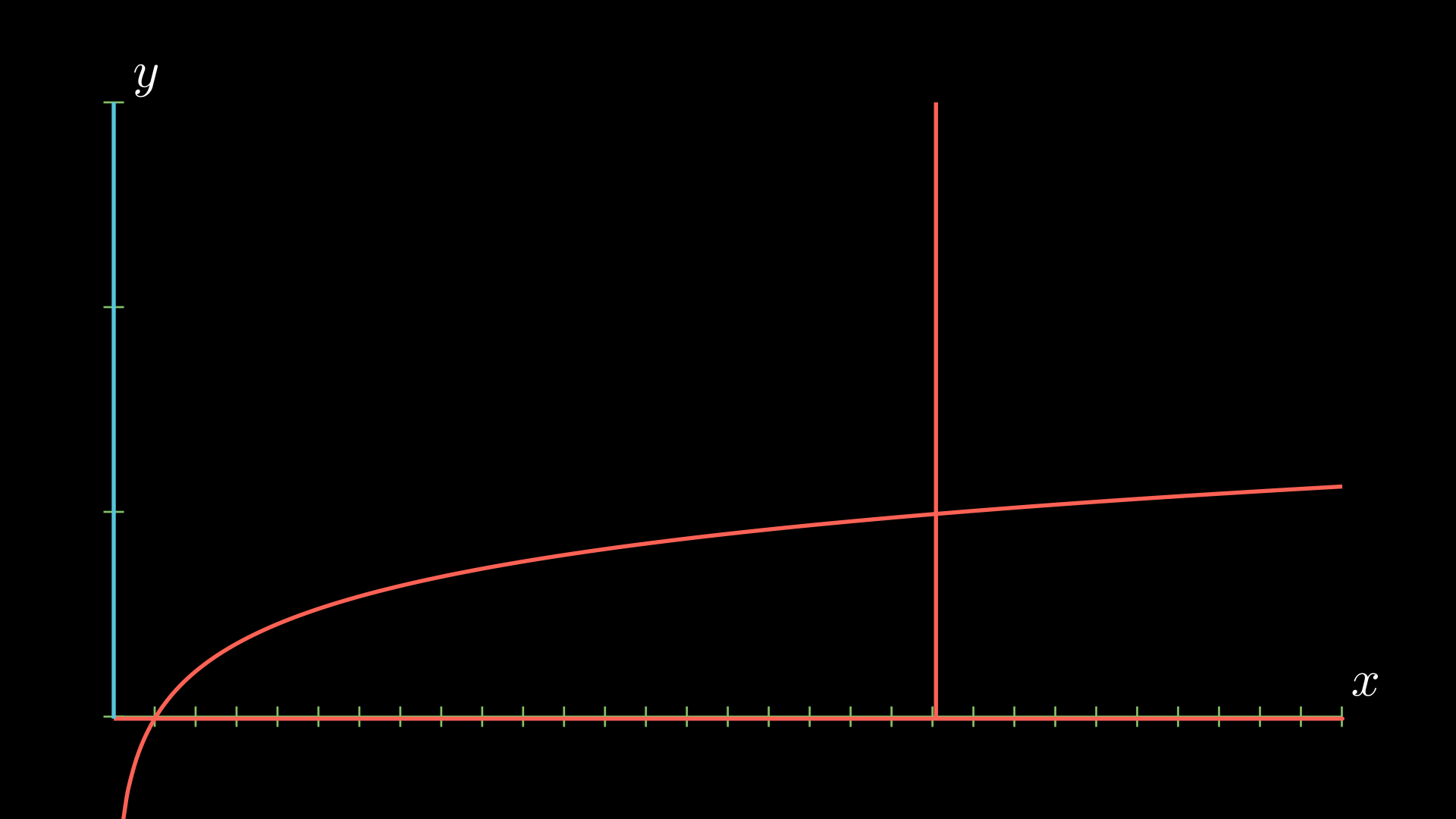
Let’s suppose that we wish to rotate this around the \(y\)-axis (so around the line \(x=0\)), which we shade with blue above. We’ll break this up into two different steps.

Washer Method

The “more natural” of the two methods is the washer method (or at least the method that students like more). The idea is that we’re going to take “slices” which are perpendicular to the axis of rotation. In this case, we fix a \(y\) and we consider a line segment connecting our axis of revolution to our region.

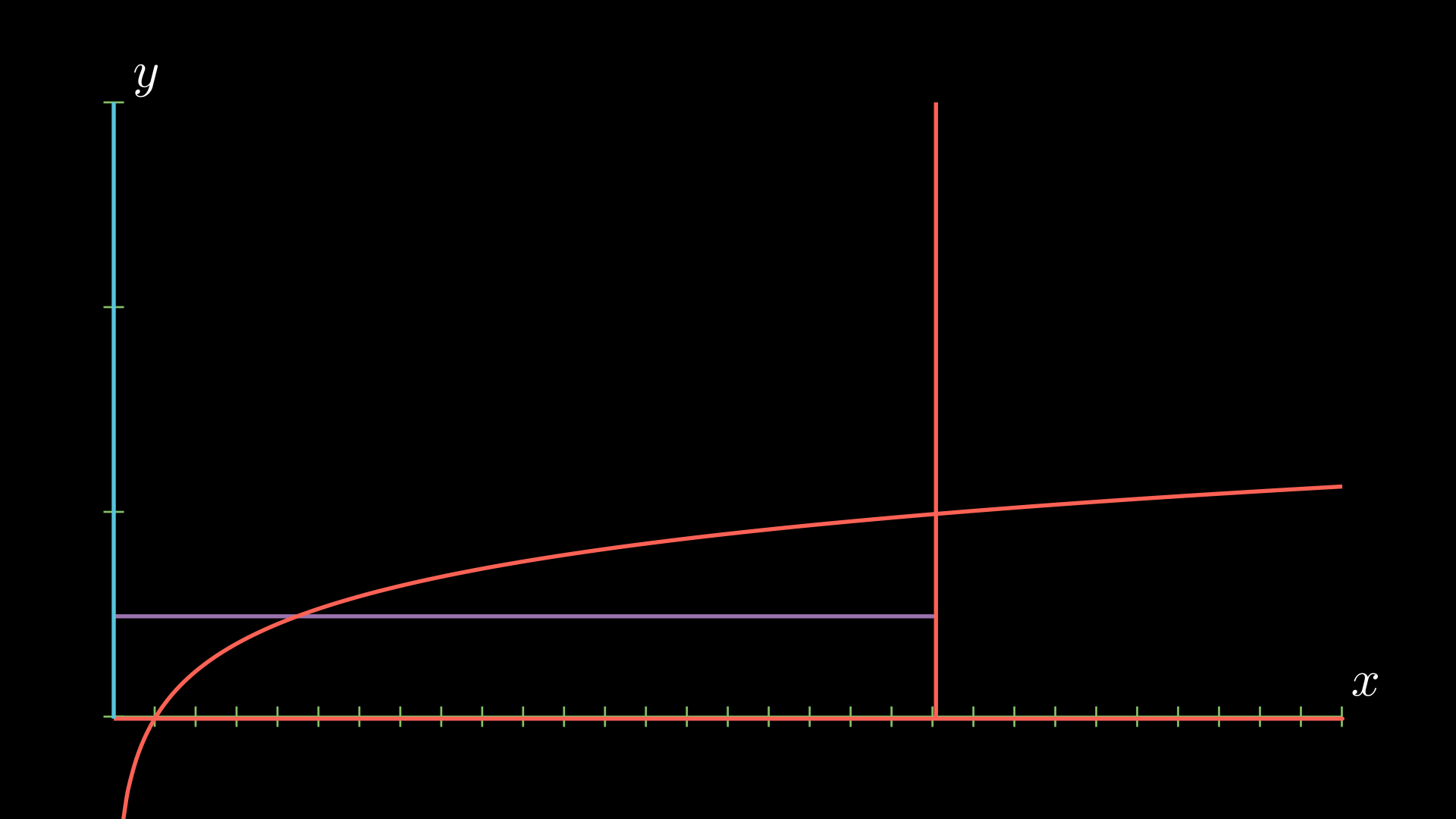
This line segment is purple above. Now, when we rotate this around, we have that the radius of the “outside circle” is given by \(R(y)\) and the radius of the “inside” circle is given by \(r(y)\).

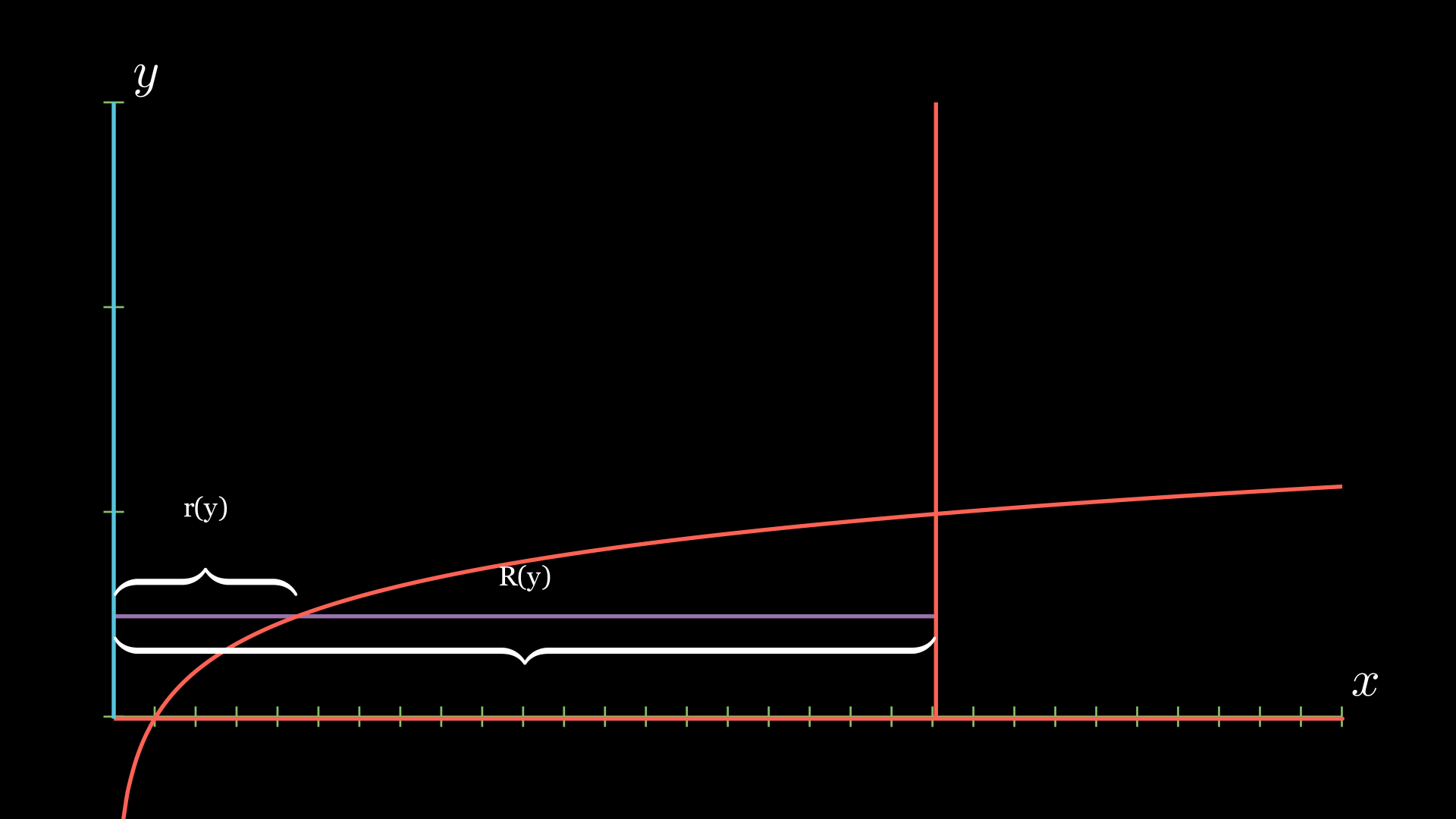
Finally, just like last time, we calculate the volume. We can do this by calculating the volume of the outside minus the volume of the inside. In our above example, the volume of the outside will be given by

\[V_{\text{outside}} = \pi \int_0^1 R^2(y) dy = \pi \int_0^1 e^{6}dy,\]

while

\[V_{\text{inside}} = \pi \int_0^1 r^2(y) dy = \pi \int_0^1 e^{6y}dy.\]

The total volume will be given by

\[V = V_{\text{outside}} - V_{\text{inside}}.\]

Shell Method

Similar to the washer method, we’re going to calculate the volume by calculating the surface area at each step and then “adding up” (i.e. integrating) the surface areas. This will be done by taking “slices” which are parallel to the axis of rotation. In this case, we fix an \(x\) and we consider the line segment connecting the two boundaries of the region. This is denoted with a purple line.

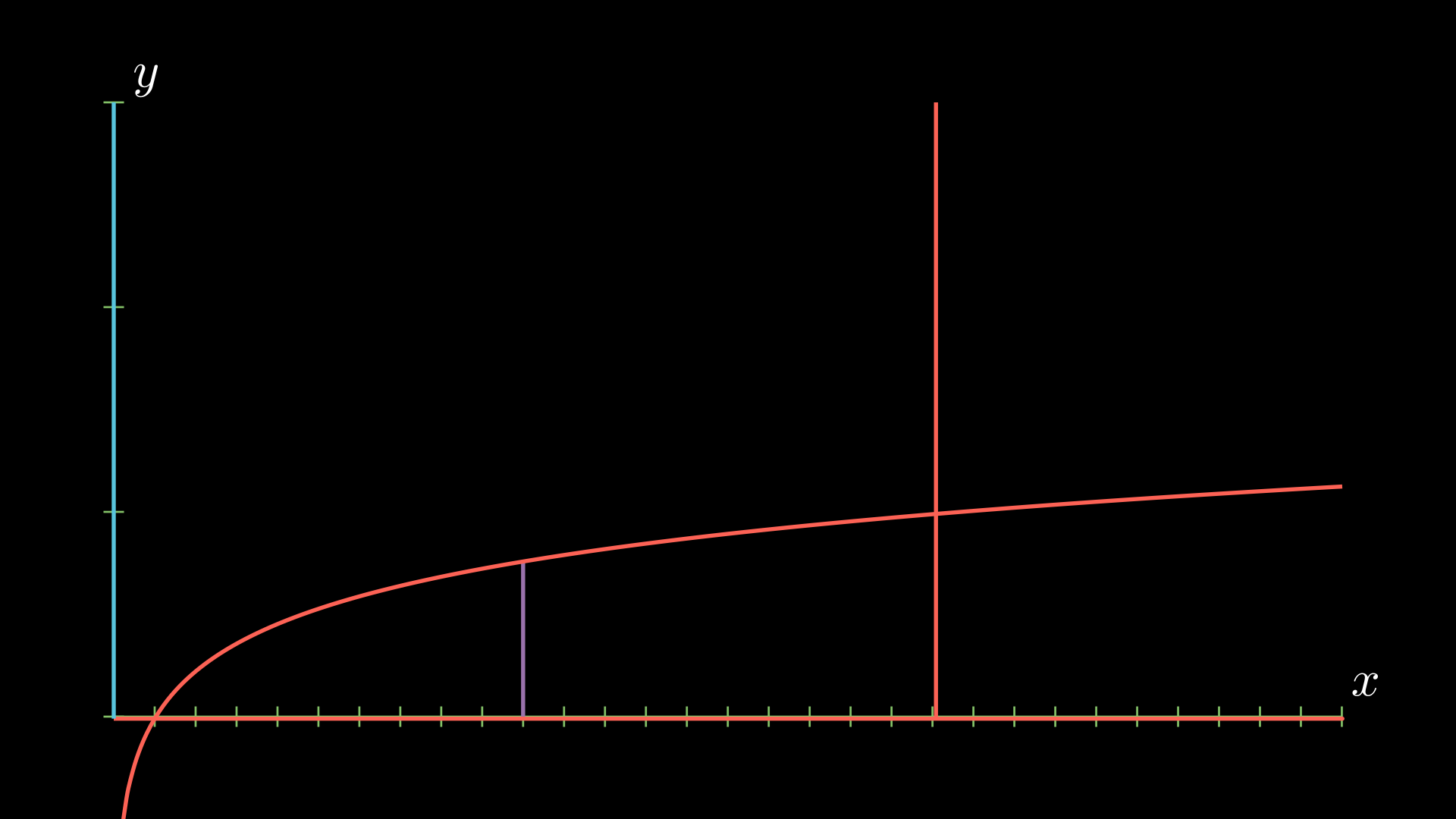
Now, we’ll need to find the surface area at a point. Imagining this like a cylinder, we’ll need to find the radius of the cylinder and the height. The height will be given by the purple line (my animation software won’t let me add a vertical brace). We can calculate this to be

\[h(x) = \frac{1}{3} \ln(x).\]

Next, we’ll need to find the radius at a point \(x\). For the \(x\)-slice defined by the purple line, this will be given by the following.

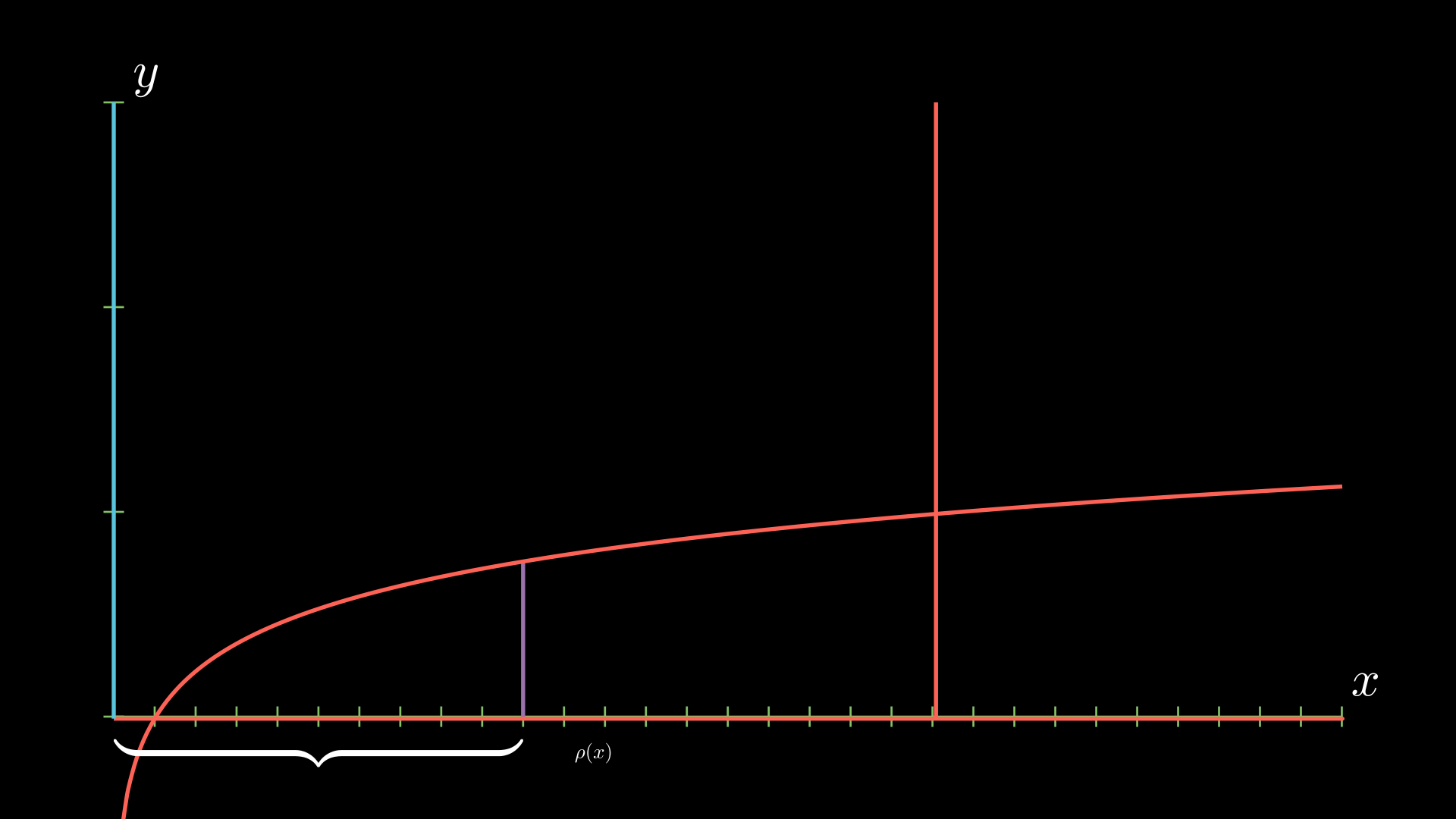
We can calculate the radius as

\[\rho(x) = x - 0 = x.\]

Finally, to find the volume, we integrate this:

\[V = 2\pi \int_1^{e^3} \left( \frac{\ln(x)}{3}\right)x dx.\]