In this recitation, we covered problems from “Volume By Slicing Handout” and the Ximera homework.

Volume by Slicing

The idea is pretty elegant assuming we have a nice set up. The idea is to take a region \(R\) and create a 3D shape by adding a 2D shape coming out of the region. More precisely, if we have a region \(R\) which is defined by two functions \(f(x)\) and \(g(x)\) on an interval \(a \leq x \leq b\), then we can create a 3D shape by attaching a 2D shape along the line connecting \(f(x)\) and \(g(x)\) at every \(x\). See the below figure (credit to Ximera), where we attach a square between the functions.

By finding the area of each shape, we can find the total volume of the solid by “adding them up.” Technically, these are infinitesmally small things, so we’re adding up infinitely many things. We (hopefully) learned in Calculus One that this can be done precisely by using an integral. In particular, if we sort of “fatten these up” by an infinitesmal amount \(dx\), we can calculate these volumes and add them up:

\[\int_a^b A(x) dx,\]

where \(A(x)\) is the area of the shape at the point \(x\). See the following picture for an example of what this looks like:

There are a few common shapes they like to look at, so it is important to know the area.

• If we have a square with side \(z\), then the area of the square is \(z^2\).
• If we have an equilateral triangle with sides \(z\), then the area is \((\sqrt{3}/4)z^2\).
• If we have a (right) isosceles triangle with one of the equal sides having length \(z\), then the area is \((1/2)z^2\).
• If we have a semicircle (meaning half a circle) with radius \(z\), then the area is \((\pi/2)z^2\).

Note that the last one is somewhat of a trick. Most of the time, we’ll be finding the diameter \(d\), not the radius. If you want to find the area of the circle in terms of the diameter, we have to use the fact that it is twice the radius:

\[d = 2z \implies \text{Area} = \frac{\pi}{8} d^2.\]

Problem: Suppose the base of a solid is a circle with radius \(4\) and the cross-sections through the solid taken parallel to the \(x\)-axis are isosceles right triangles. Set up an integral to compute the volume.

Solution: Step one is to always draw a picture. Since we have a circle with radius \(4\), we can draw it on a computer by using the relation \(x^2 + y^2 = 4^2 = 16\). If we’re going to plot this, we’re going to have to use the fact that this relation is really two functions: \(y = \pm \sqrt{16 - x^2}\). We get the following picture

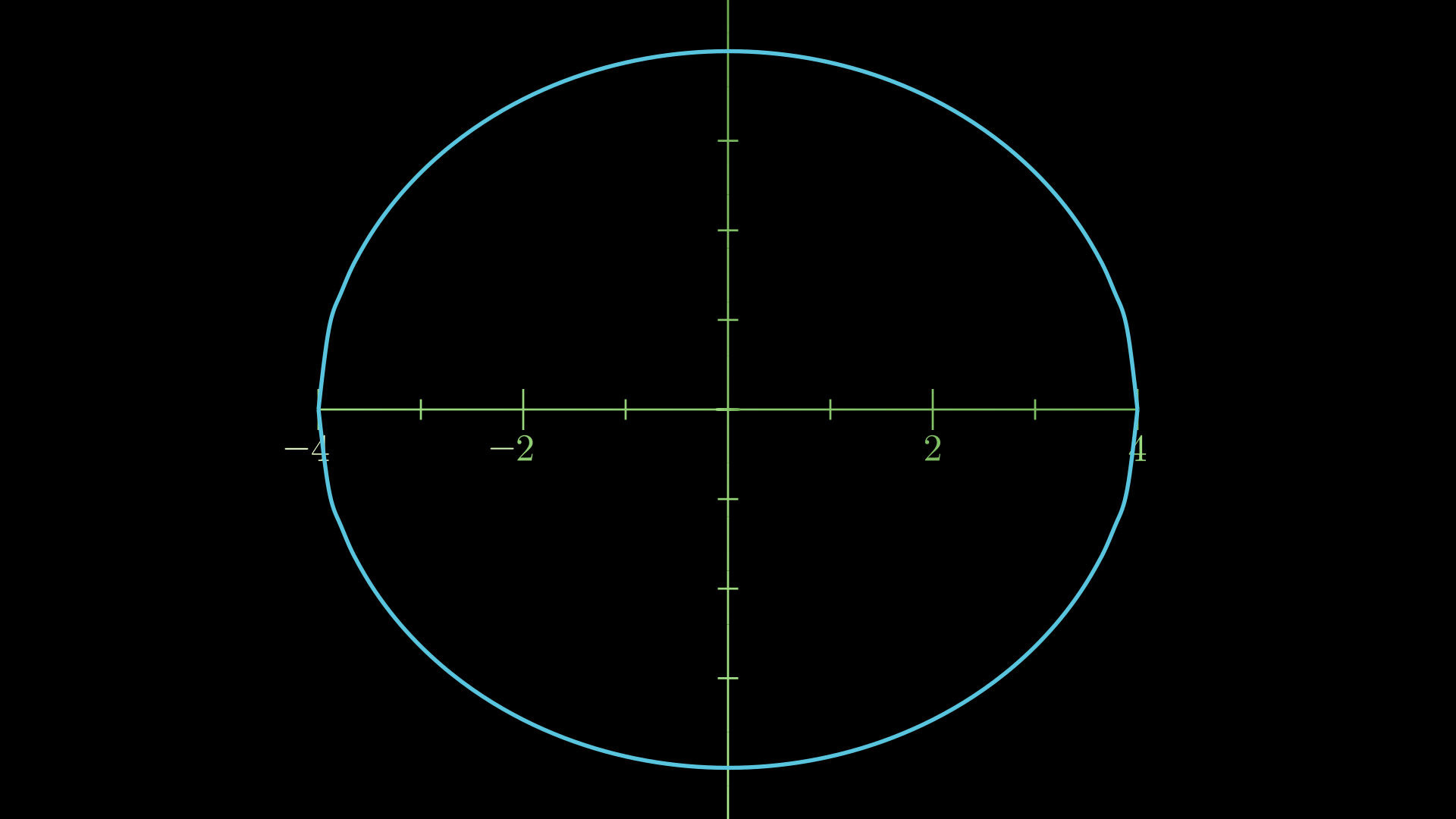
Now, if the cross-sections are parallel to the \(x\)-axis, then at any given \(y\)-value we have the following picture:

So to set up the integral, we will need to integrate from \(-4\) to \(4\) the area of these triangles. The area of each triangle will be

\[\frac{1}{2}(\sqrt{16 - y^2} - (-\sqrt{16 - y^2}))^2 = 2 (16 - y^2).\]

Therefore, the volume will be

\[\int_{-4}^4 2 (16 - y^2)dy.\]