In this recitation, we covered problems from the mock quiz.

Mock Quiz

Problem: Consider the region \(R\) bounded by \(y = \sqrt{x}\), \(x + 10y = 11\), and \(y=0\). This region forms the base of a solid \(S\). Taking cross-sections through the base to be squares which are parallel to the \(x\)-axis,

1) calculate the volume of the solid, and

2) find a value of \(a\) so that the volume of the solid to the left of the line \(x=a\) is equal to the volume of the solid to the right of \(x=a\).

Solution: As always, we’re going to start by plotting the region. We have the following.

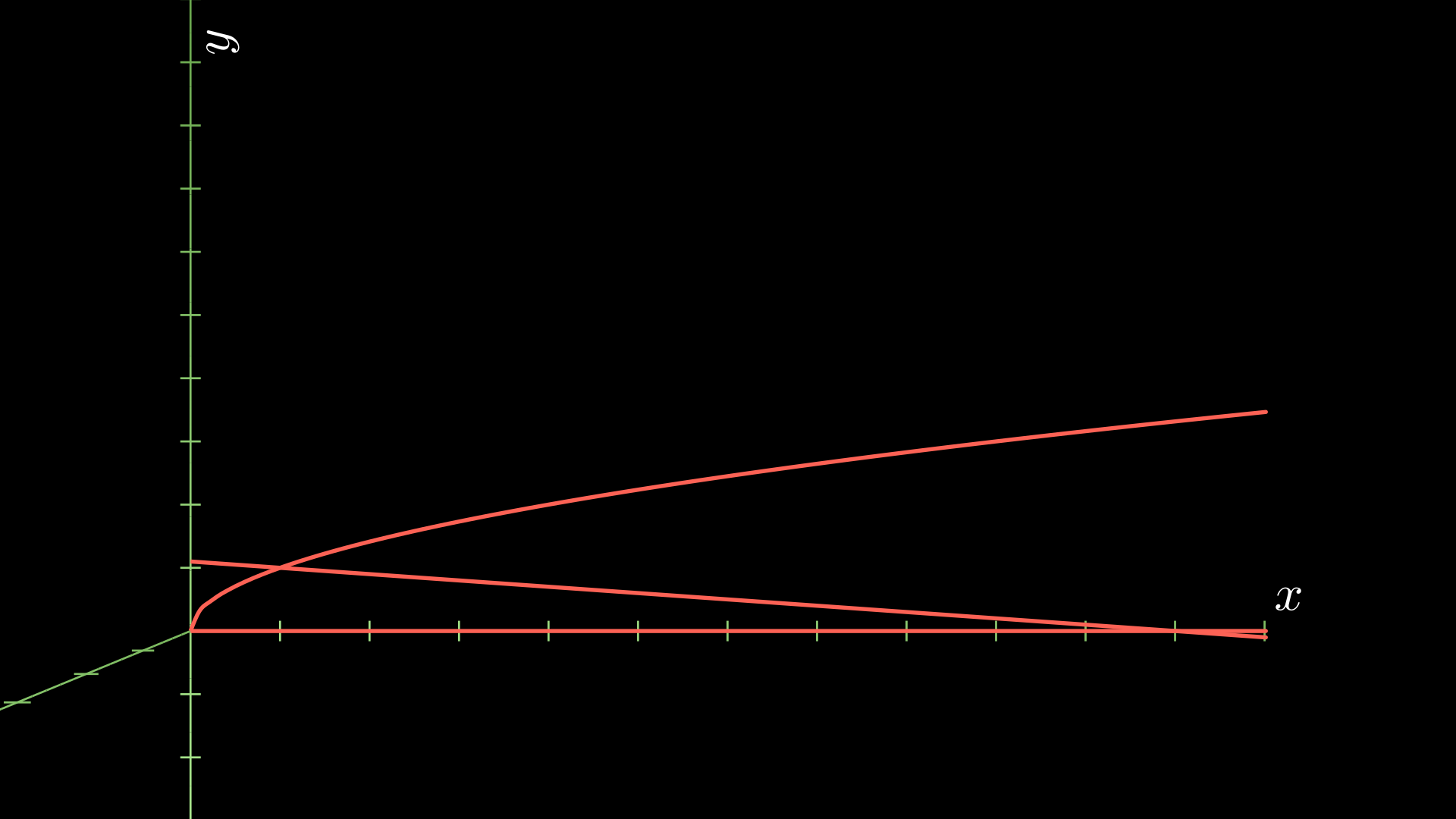
Next, our cross sections are going to be parallel to the \(x\)-axis, so we are integrating with respect to \(y\). It will be useful to find the inverse functions of the functions defining our region. We have

\[x = y^2 \text{ and } x = 11-10y.\]

At some given \(y\)-value, we now draw the picture of the square cross-section:

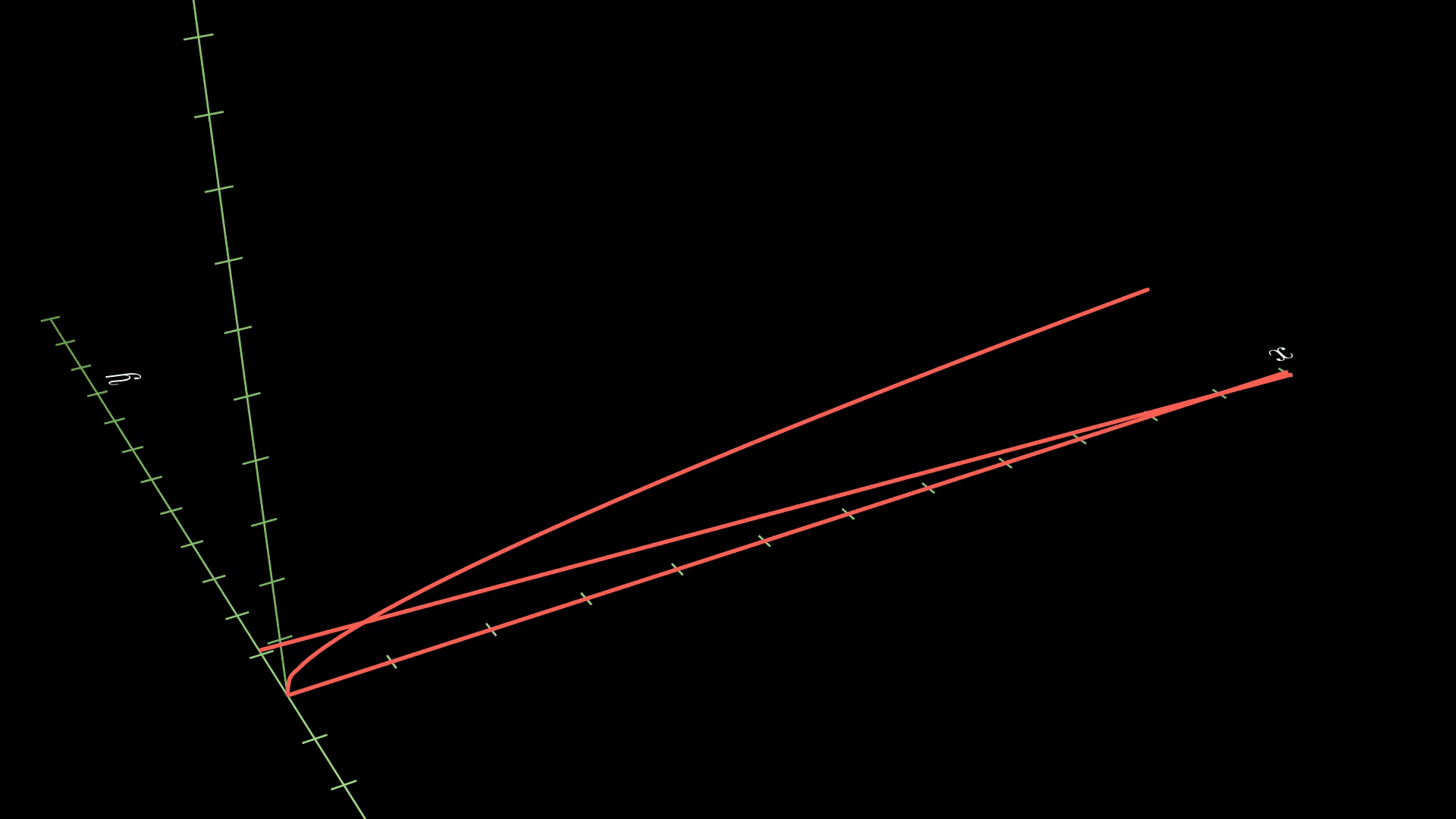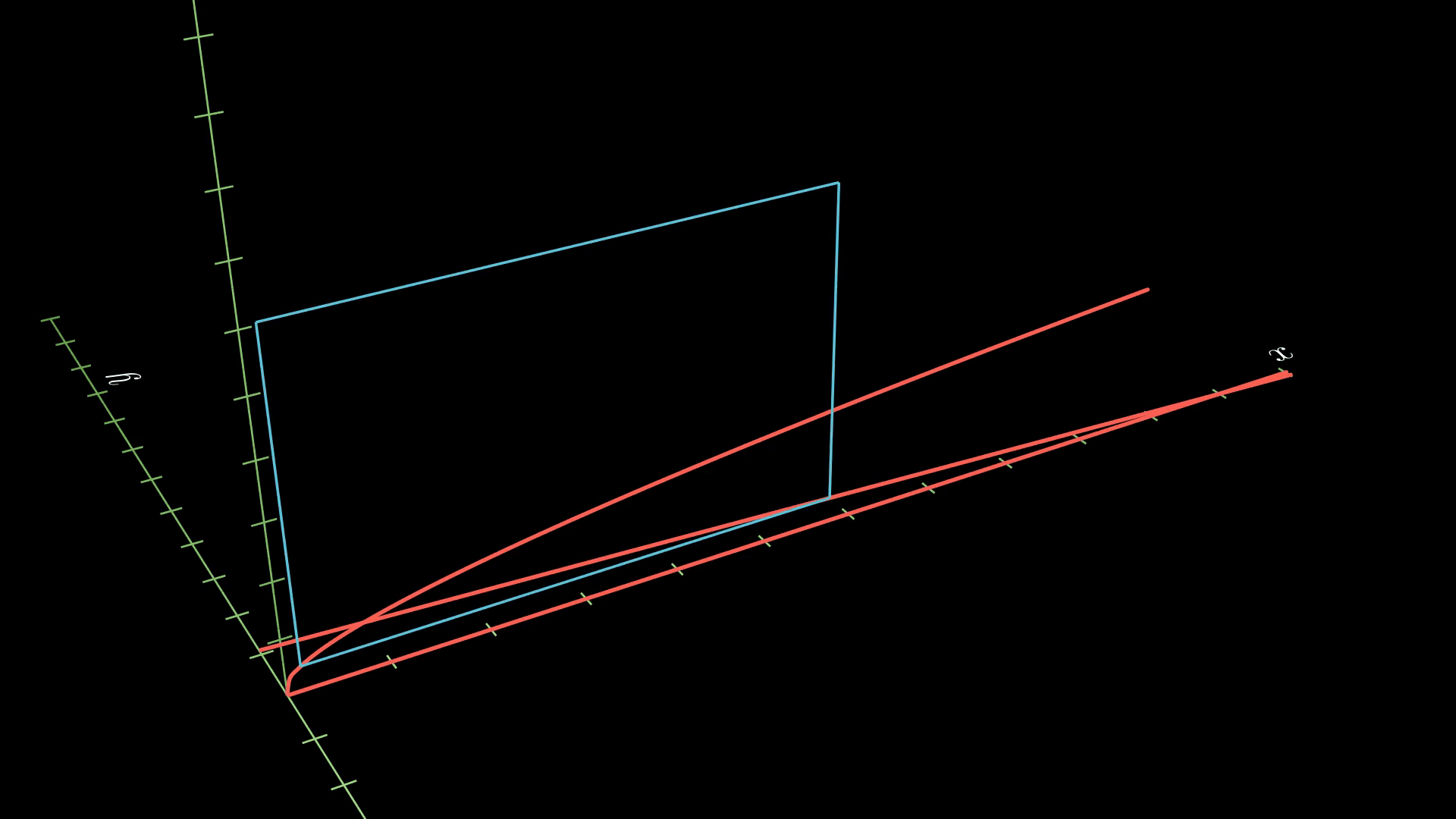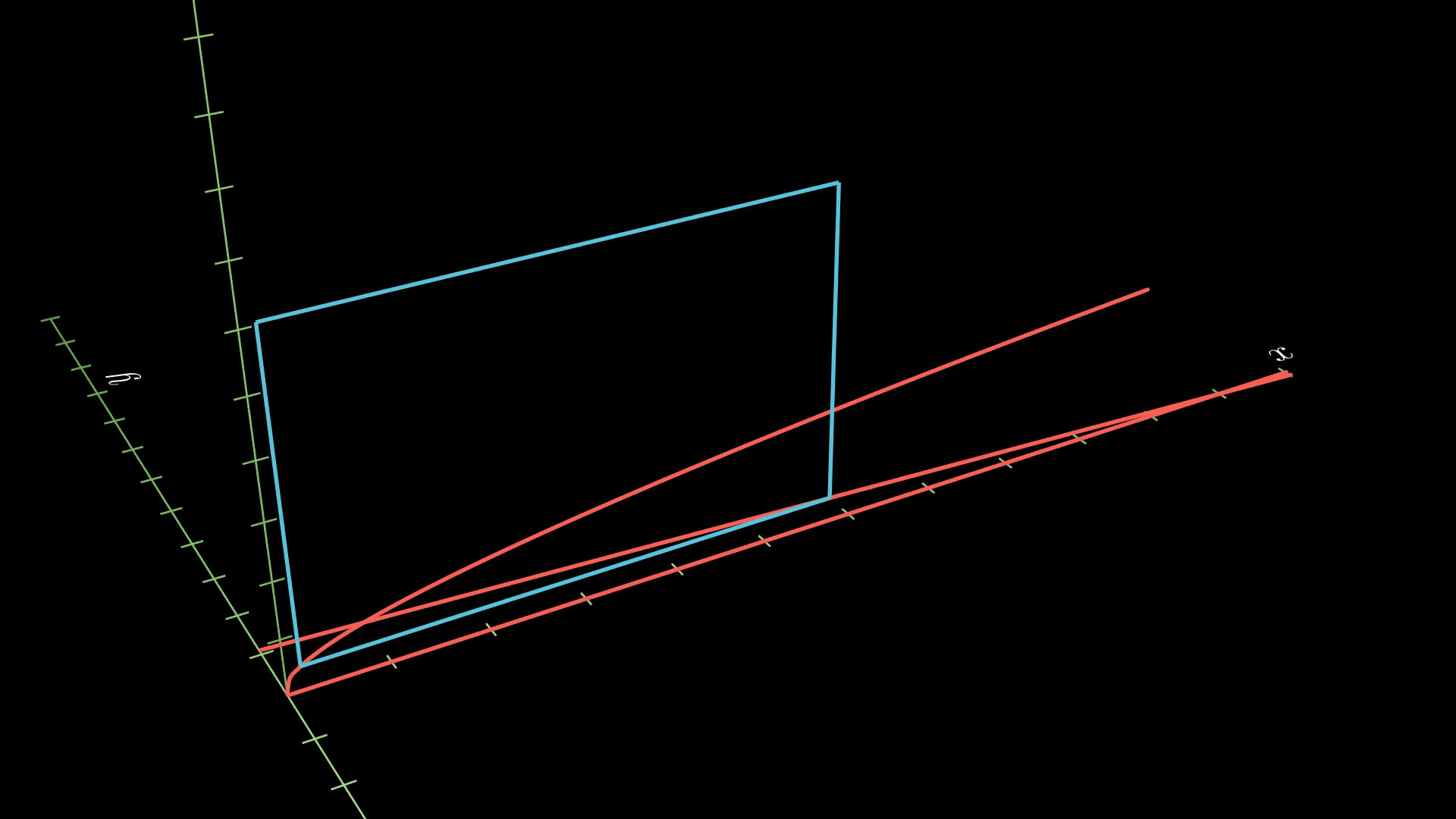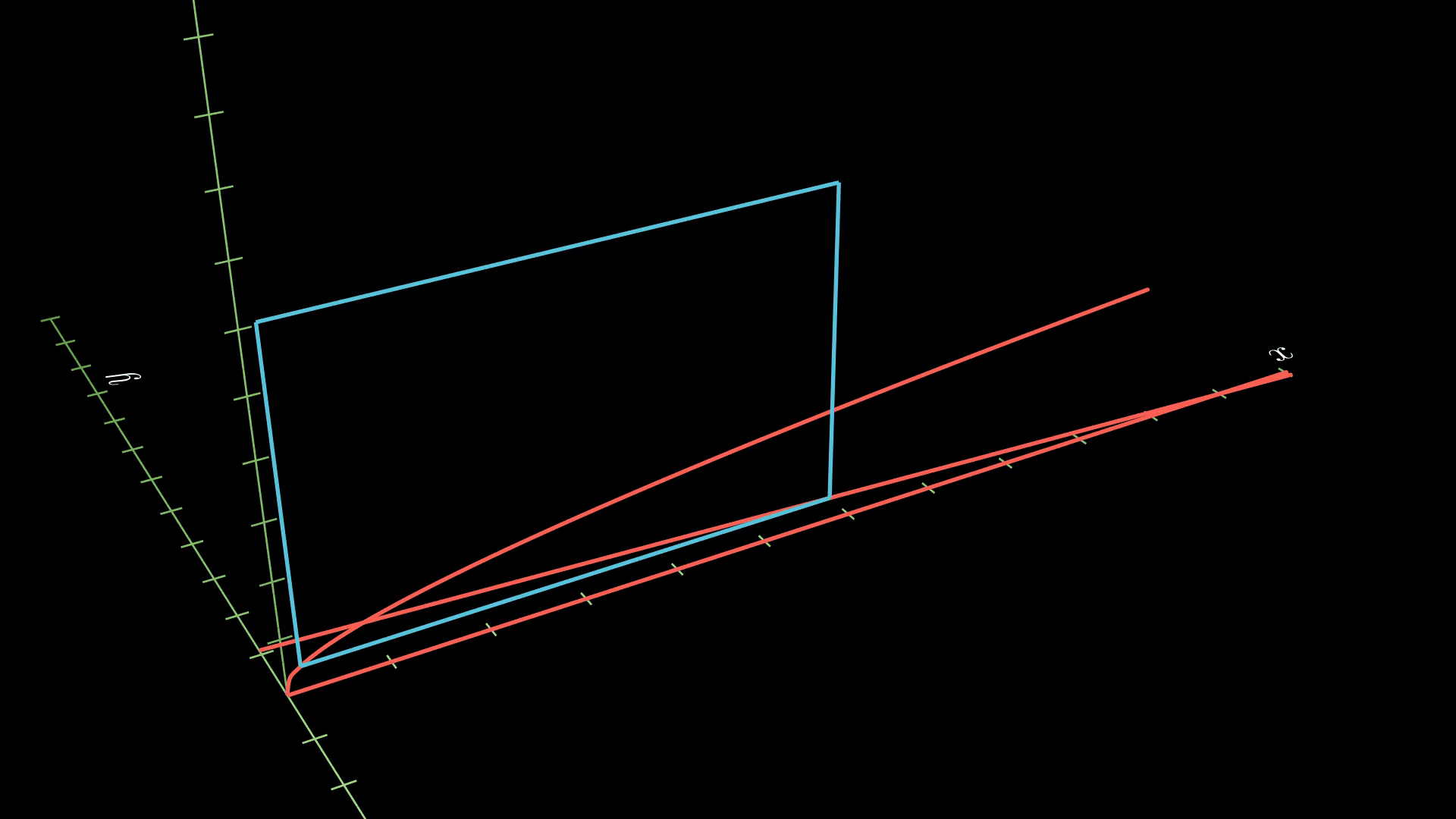
We see that the area at a given \(y\) is given by

\[A(y) = (11 - 10y - y^2)^2.\]

Finally, the last bit of information we’re missing is the upper bound for \(y\). Notice this happens when

\[11 - 10y = y^2.\]

Solving this yields \(y = -11\) and \(y = 1\) as the two intersection points. Since we’re in the first quadrant, the intersection point we care about is \(y=1\). Putting it all together, we have that the volume is

\[\int_0^1 (11-10y-y^2)^2 dy = \frac{211}{5}.\]

To solve the next part, we need to fix a line \(x=a\). Let’s assume \(a \geq 1\) and add this to our region. This will be the green line below.

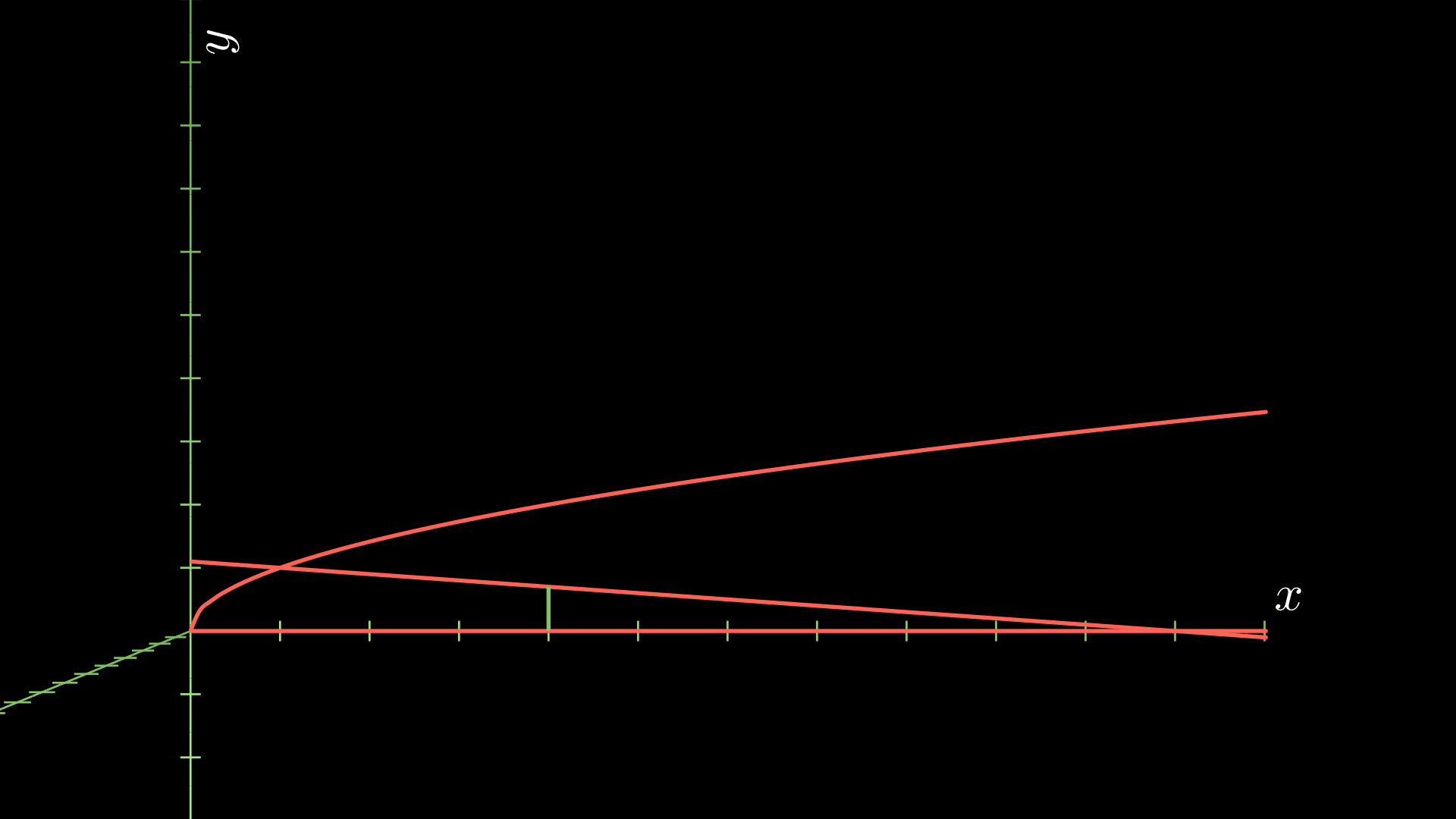
Now, we want to find an \(a\) value so that the volume of the solid to the right of the line is the same as the volume to the solid of the left of the line. Since it’s the same volume, they have to add up to the total volume. So we just need to figure out when the volume to the right of the solid is equal to half of the total volume.

To construct a cross-section for the volume of the solid to the right of the line, we will need to use a rectangle instead of a square, as you can see in the following animation.

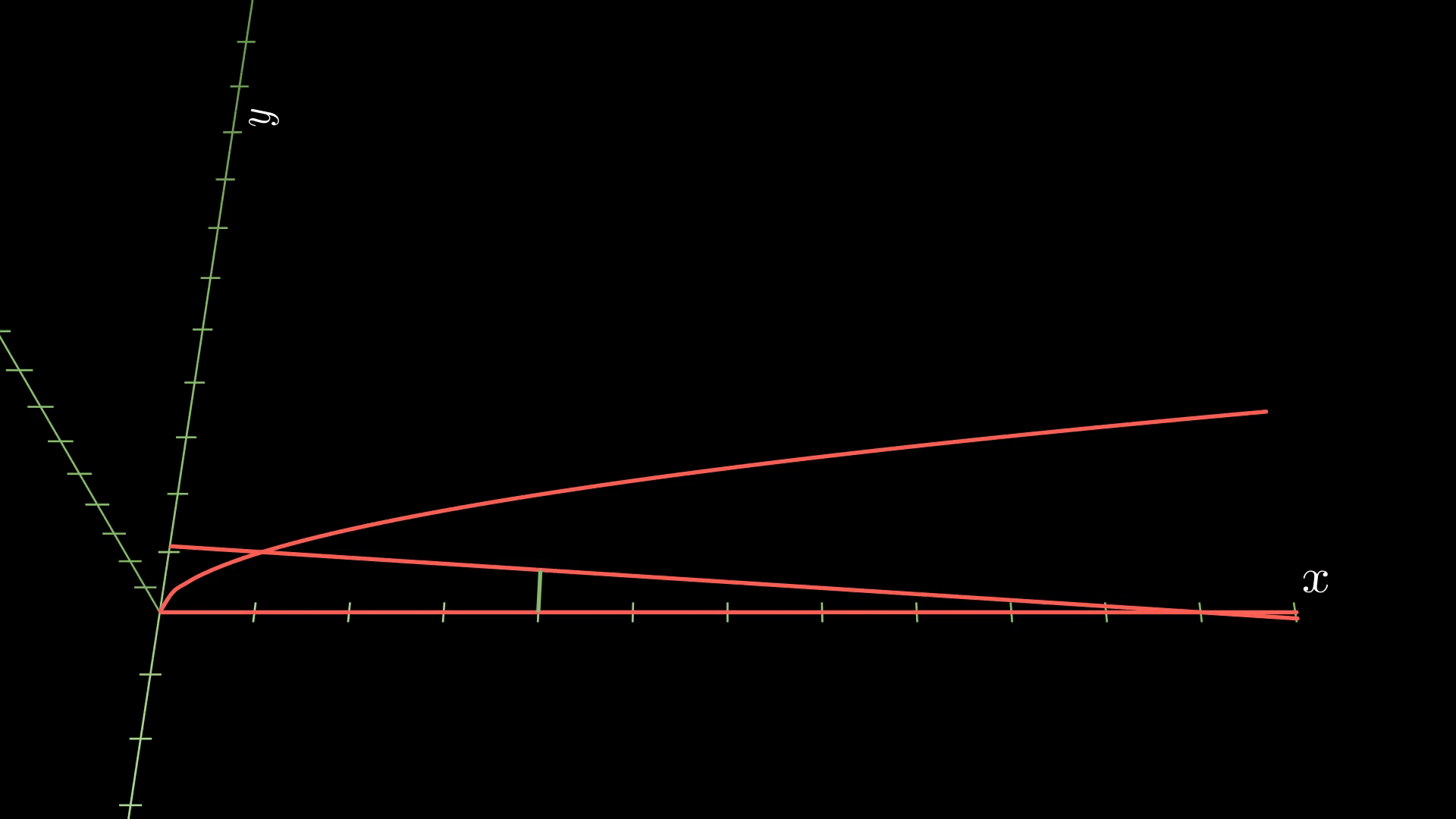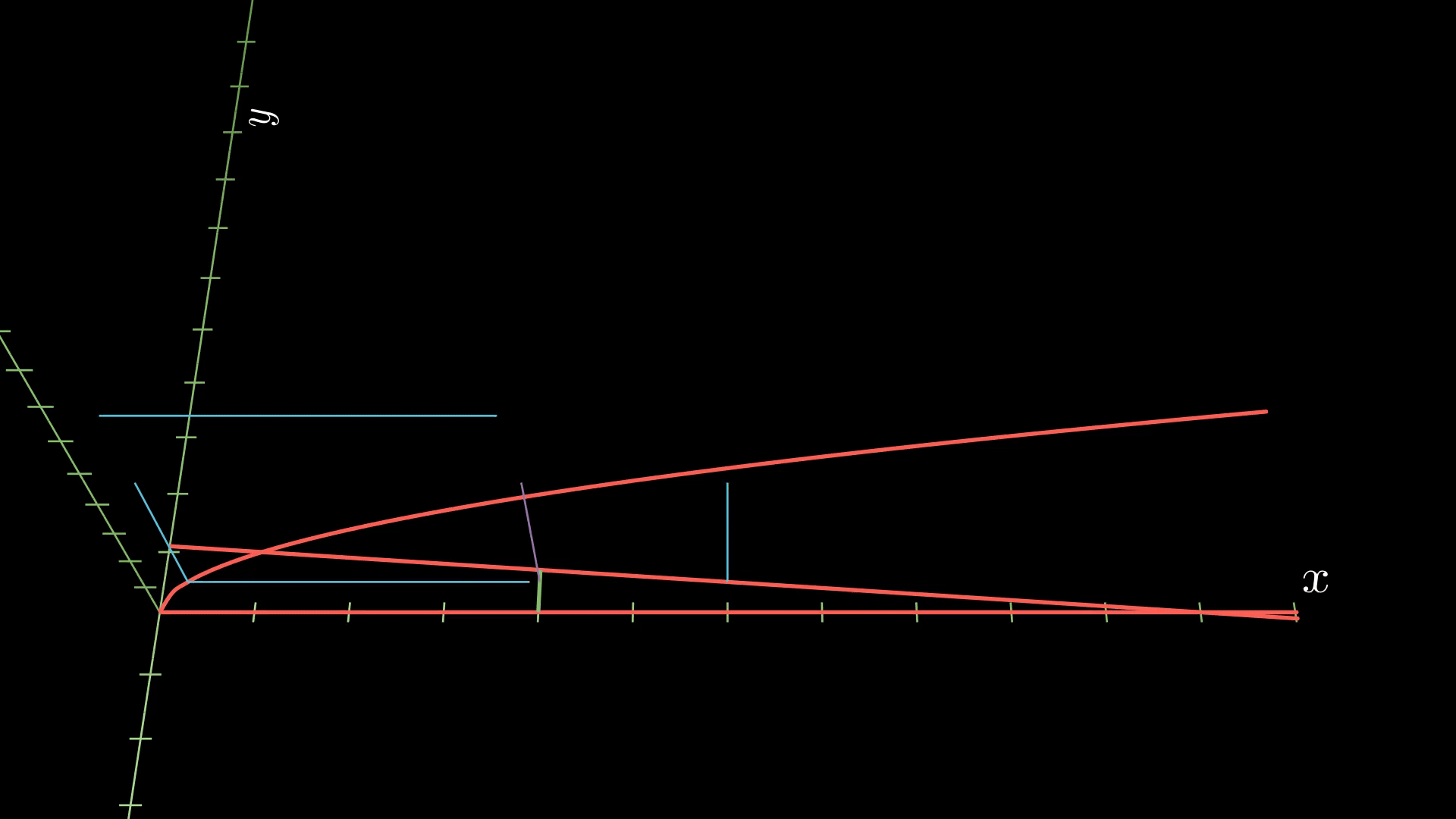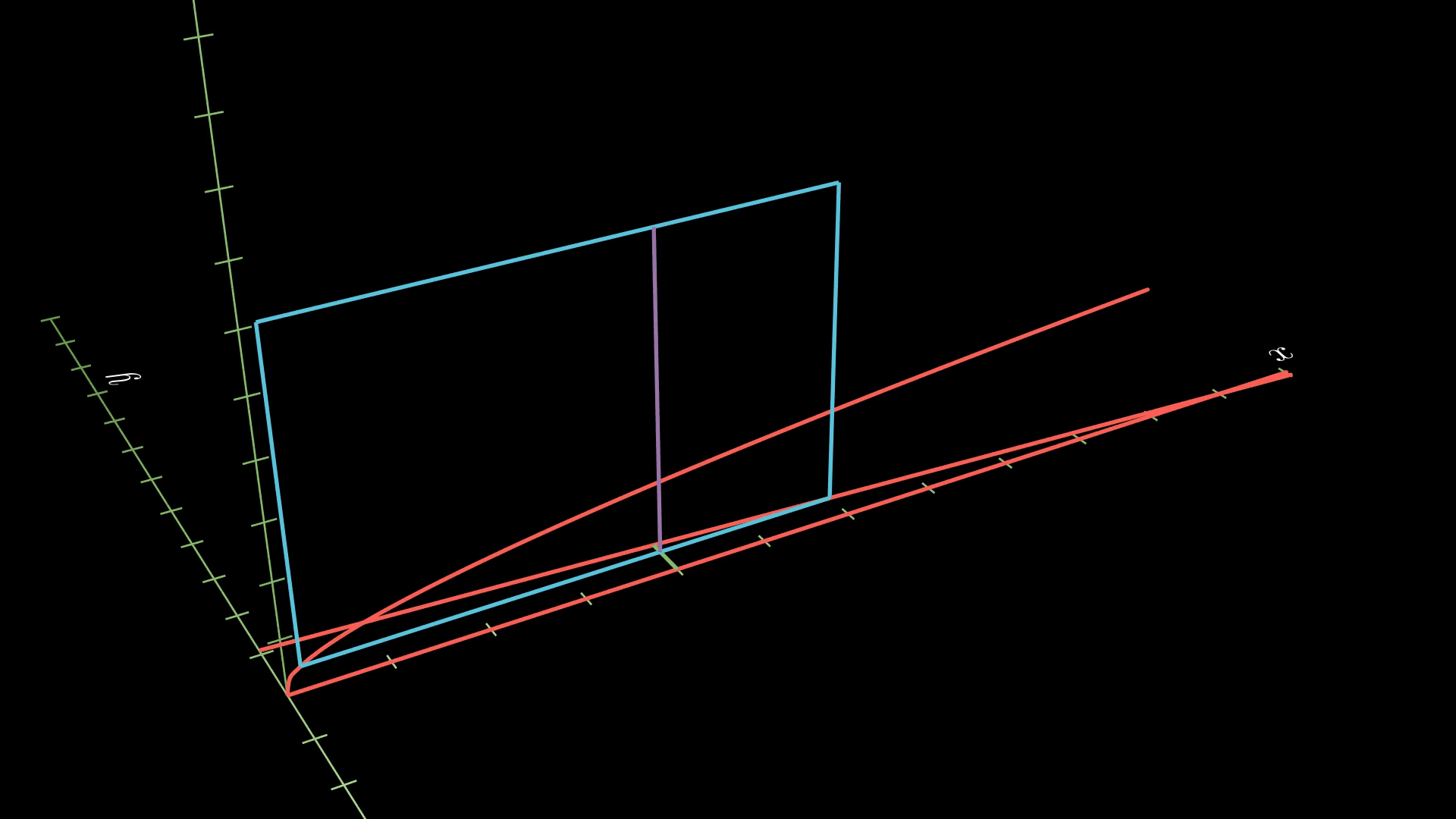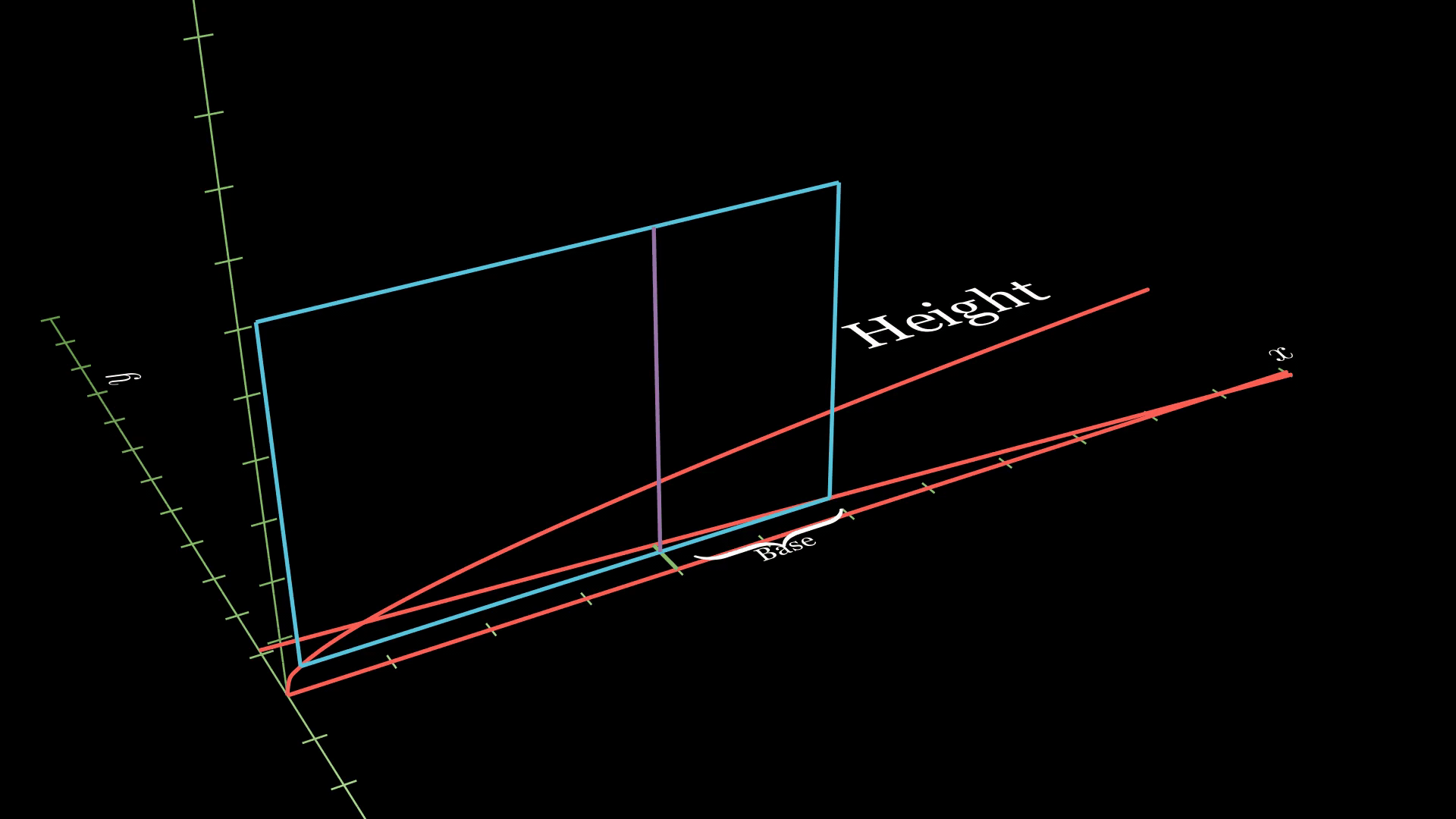
So the area of a cross-section is given by base times height, or

\[A(y) = (11-10y-y^2) (11-10y-a).\]

To integrate, we have the lower bound \(0\), but we need to find the upper bound. This will occur where \(x=a\) intersects \(x = 10 - 11y\). Solving this for \(y\) gives us

\[y = \frac{11-a}{10}.\]

Putting it all together, the volume of the solid to the right is given by

\[\int_0^1 (11-10y-y^2) (11-10y-a)dy.\]

Expanding out the inside, this is the same as

\[\int_0^1 [(121 - 11a) + (10a-220)y + (89+a)y^2 + 10y^3]dy.\]

Using the power rule and substituting, we get that the volume to the right of the line is

\[-\frac{(a-11)^2(a^2-22a-4279)}{12000}.\]

To figure out the \(a\) value, we set this equal to half of the total volume. Thus

\[-\frac{(a-11)^2(a^2-22a-4279)}{12000} = \frac{211}{10}.\]

Using a calculator, we see that \(a \approx 3.987\).