Below are some fun animations I’ve done recently using Matplotlib, Python, and Maple.

Animation of Jacob Bernoulli’s Solution to the Harpsichord Problem

Plot of \(u(x,t)\) with initial condition \(u(x,0) = f(x),\) \(\frac{\partial u}{\partial t} \bigg|_{t = 0} = 0,\)

and initial condition \(f(x) = \begin{cases} x \text{ for } 0 \leq x \leq \frac{\pi}{2} \\ \pi - x \text{ for } \frac{\pi}{2} \leq x \leq \pi \end{cases}\)

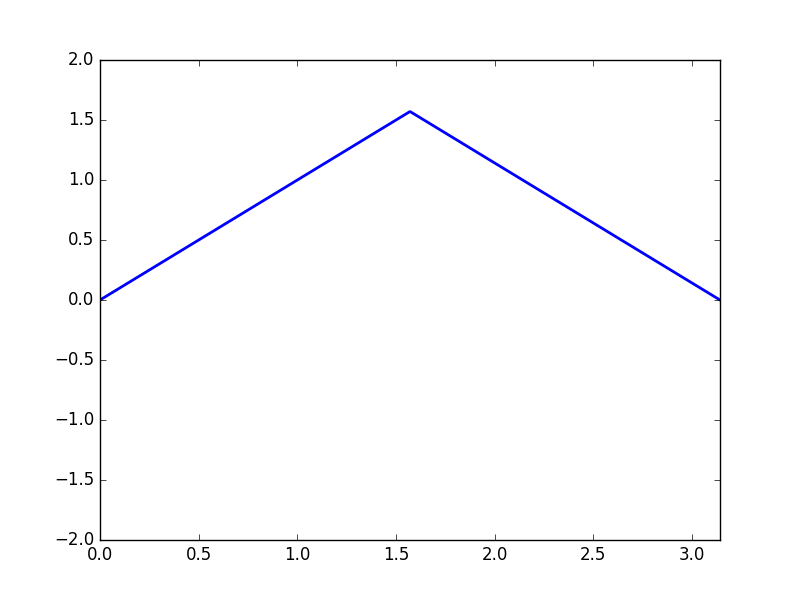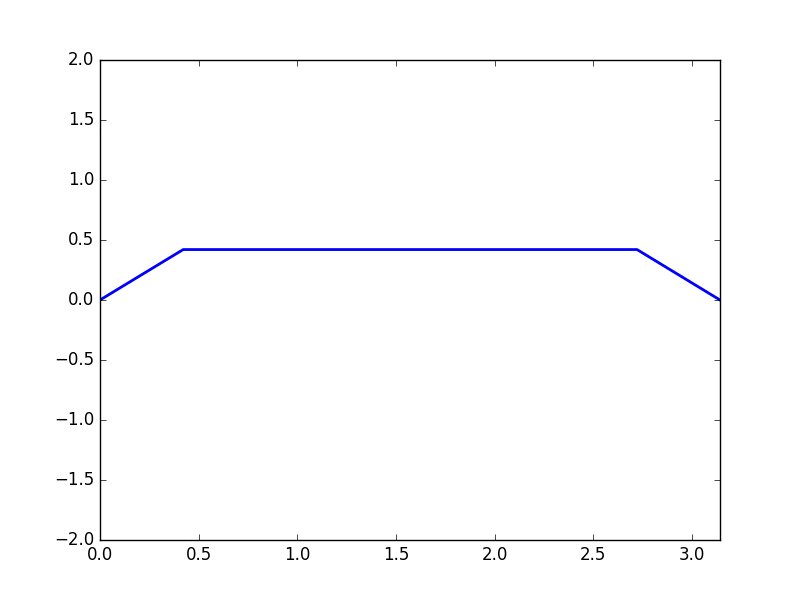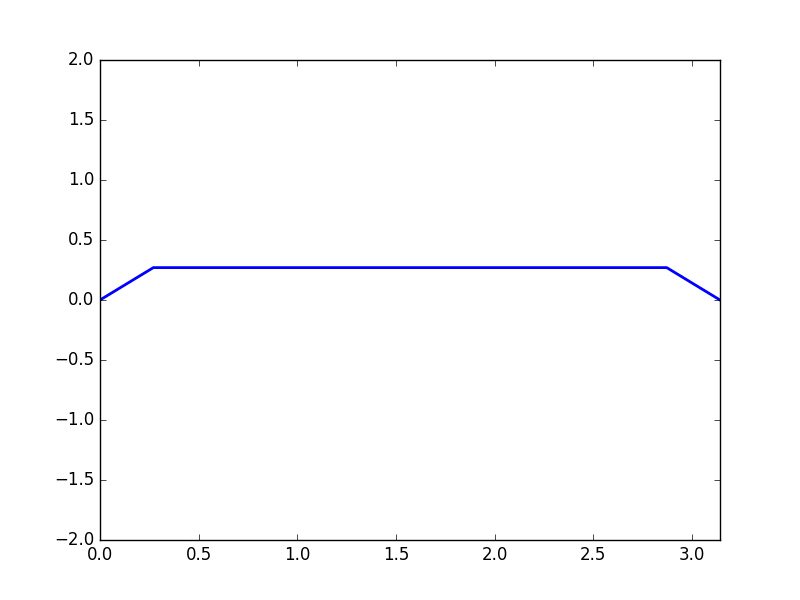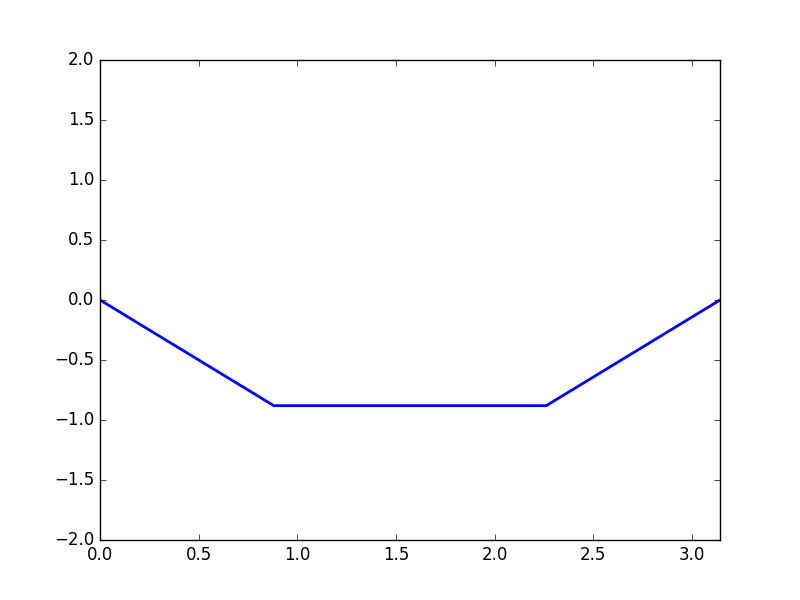
Code can be found here.

Animation of the Devil’s Staircase (Cantor Function)

Define \(C_0 = [0,1],\) and \(C_k = \frac{C_{k-1}}{3} \bigcup \left(\frac{C_{k-1}}{3} + \frac{2}{3} \right).\) Then \(C = \bigcap_{k=1}^{\infty}C_k\) is called the Cantor set. We define the Cantor function as follows; let \(D_k = [0,1] \setminus C_k.\) Then we may write D_k as a union of non-overlapping open intervals; notationally, we have \(D_k = \bigcup_{j=1}^{2^n-1} (I_j^n)^{\mathscr{o}}.\) Order these intervals in the natural way, where \(\max(I_j) \leq \min (I_{j+1}).\) Define a function \(f_n(x) = \begin{cases}\frac{j}{2^n} \text{ if } x \in (I_j^n)^{\mathscr{o}} \\ \frac{1}{2^n(\min(I_j^n) - \max(I_{j-1}^n))}x + \frac{\max(I_{j-1}^n) \frac{j}{2^n} - \min(I_j^n) \frac{j-1}{2^n}}{\max(I_{j-1}^n) - \min(I_j^n)} \ \text{ if } \max(I_{j-1}^n) \leq x \leq \min(I_j^n) \\ \text{linear between 0 and }I_1^n \text{ and 1 and }I_{2^n-1}^n \end{cases}\) Notice that for each n, we have \(|f_{n+1}(x) - f_n(x)| < 2^{-n} \ \forall x \in [0,1]\) and so we have f_n uniformly converges to a function f called the Cantor-Lebesgue function. It is animated below for \(0 \leq n < 10.\)

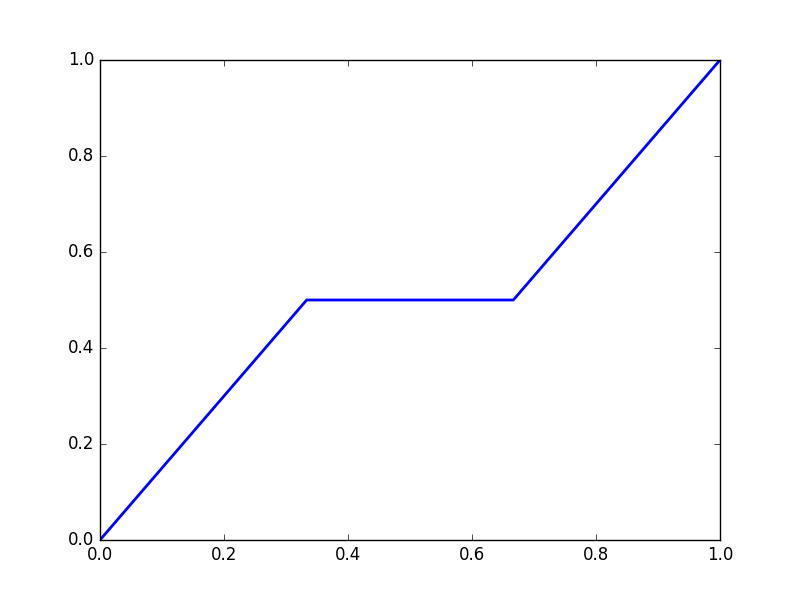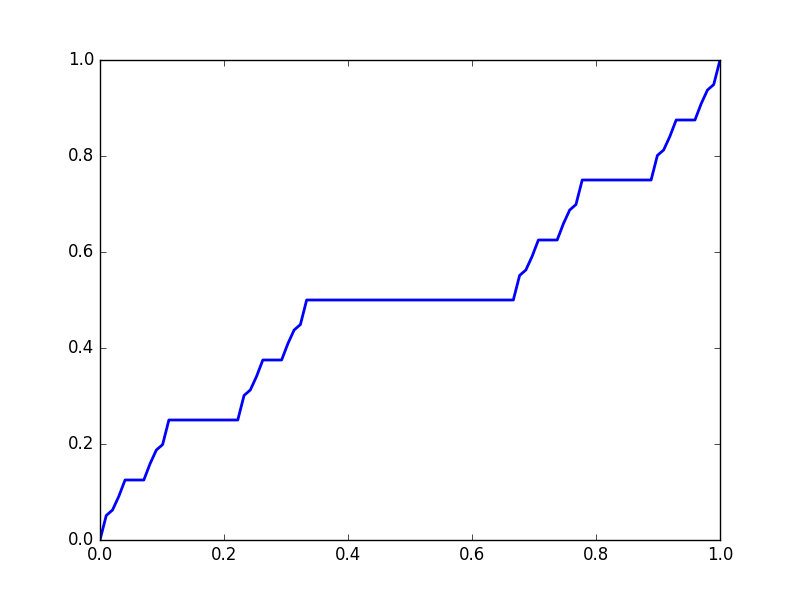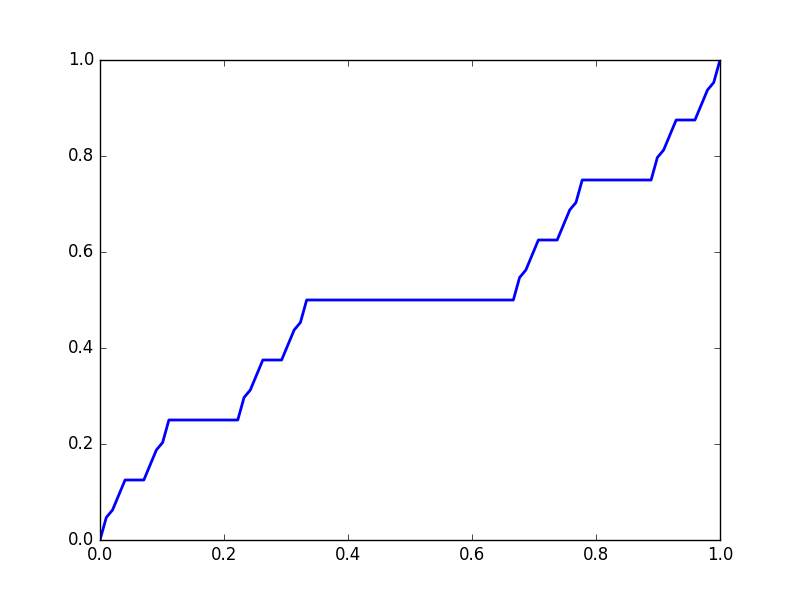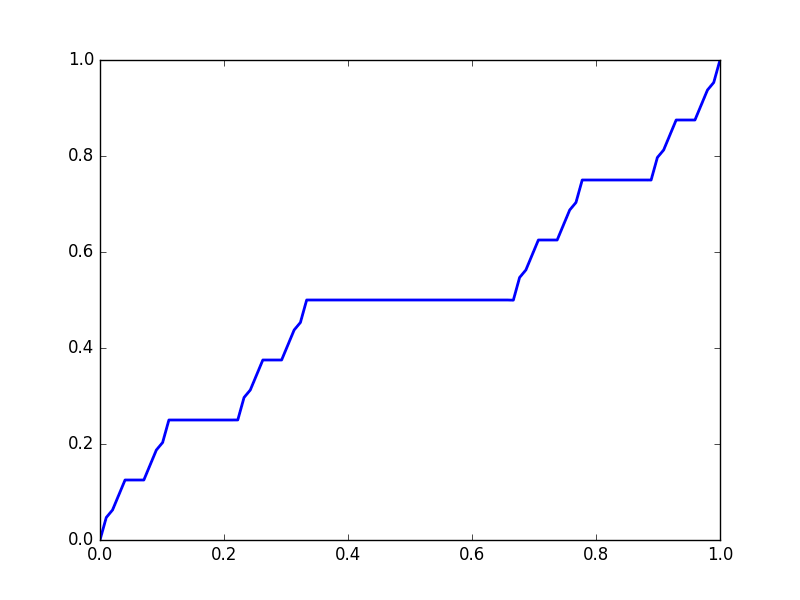
Code can be found here.

Animation of Convergence of Simple Functions

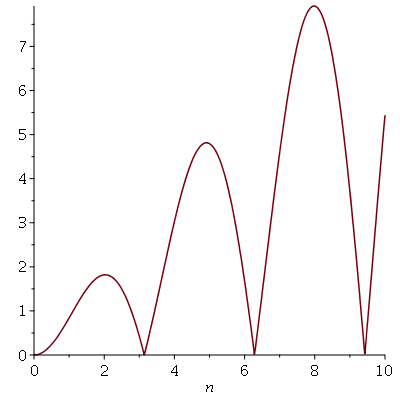
We define a simple function f to be a function which takes a finite number of (finite) values over the reals (to whatever dimension). We have a theorem which says for a function f which is always positive, we can create a sequence of simple functions which increase to the function, via setting \(f_n(x) = \sum_{j=1}^{n 2^n} \left( \left(\frac{j-1}{2^n}\right) \chi_{\{\frac{j-1}{2^n} < f \leq \frac{j}{2^n} \} } \right) + n \chi_{\{f \geq n\}}.\) To show this, I created a sequence of functions following this definition which converges to \(f(x) = |x\sin(x)|.\) You can see below the convergence for 1 <= n <= 8.</p>

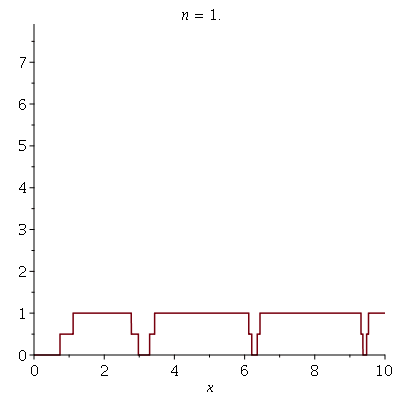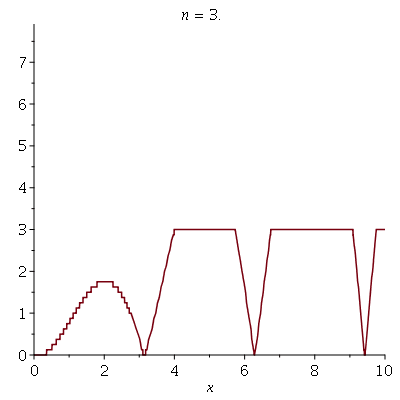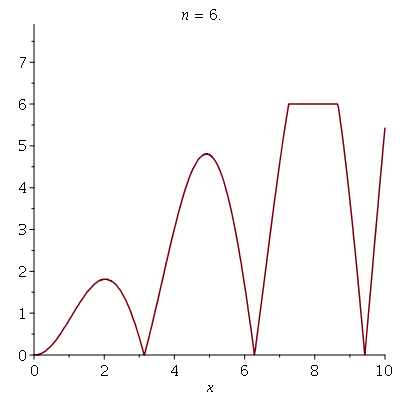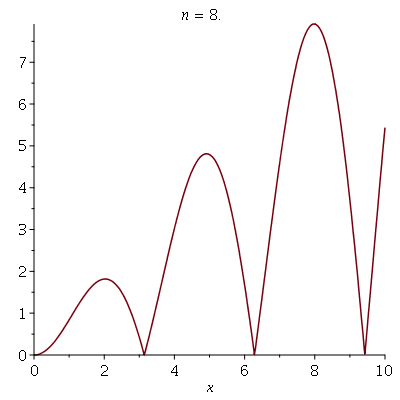
The target function is shown below.

Created using Maple.

Animation of Left Riemann Sums

Here is the animation of the convergence of left Riemann sums for the function \(f(x) = x^2\) on the interval \([0,1]\).

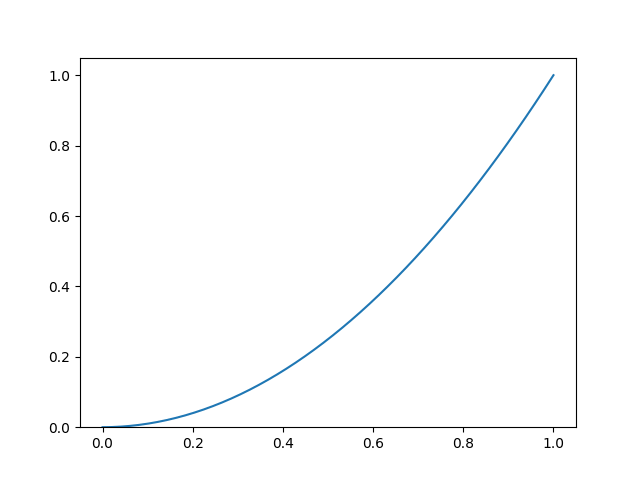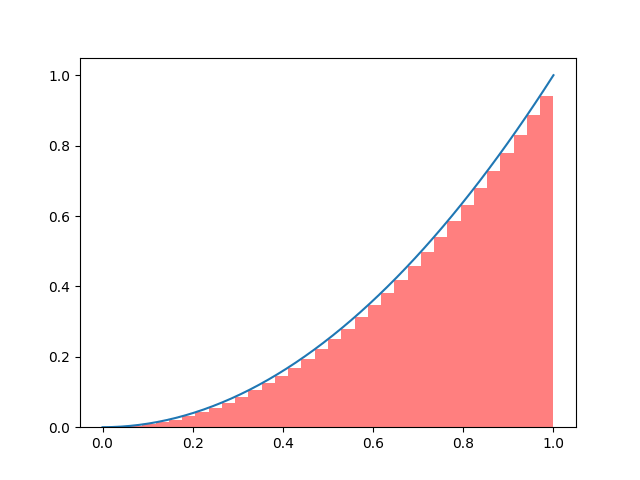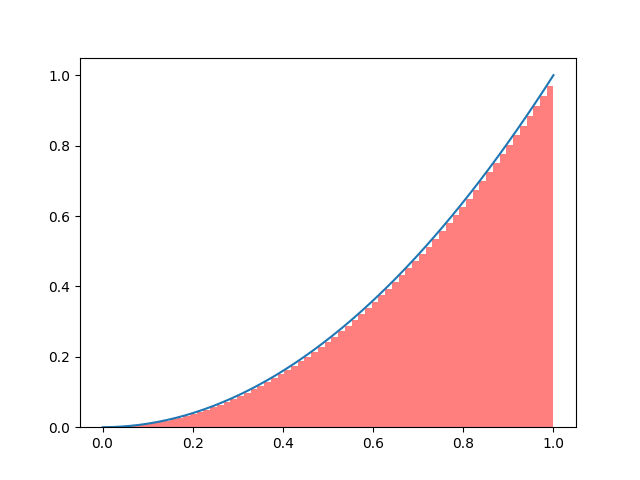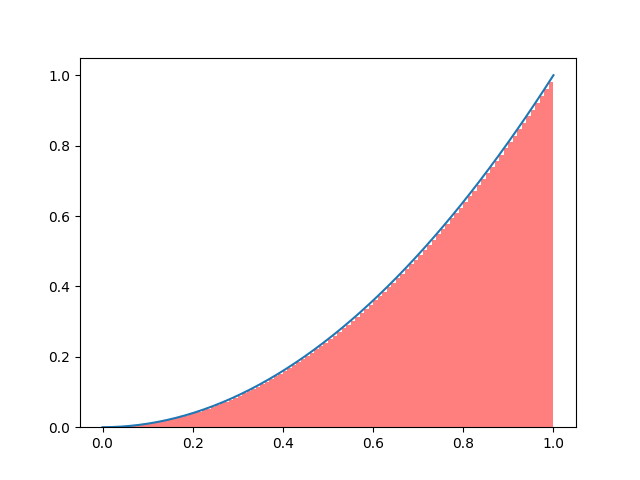
Code can be found here.